| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Ai
- GPT
- nlp
- 인공지능
- 머신러닝
- 신뢰성
- fairness
- cnn
- ML
- 딥러닝
- ChatGPT
- 지피티
- GPT-3
- 설명가능성
- trustworthiness
- Transformer
- Bert
- 인공지능 신뢰성
- gpt2
- word2vec
- AI Fairness
- 트랜스포머
- 케라스
- MLOps
- DevOps
- 챗GPT
- 챗지피티
- Tokenization
- 자연어
- XAI
- Today
- Total
research notes
확률통계(1) - 확률 본문
1. 사건과 확률
① 시행(trial)
- 몇 번이고 반복할 수 있고 결과가 우연에 좌우되는 실험이나 관측
ex) 주사위 던지기, 동전 던지기
② 표본공간(sample space)
- 어떤 시행을 했을 때 일어날 수 있는 모든 결과를 모은 집합
ex1) 주사위를 던지는 시행의 표본공간: {1, 2, 3, 4, 5, 6}
ex2) 동전을 던지는 시행의 표본공간: {앞, 뒤}
③ 사건(event)
- 표본공간의 부분집합(표본공간의 일부분)
ex1) 짝수 눈이 나오는 경우: {2, 4, 6}은 주사위를 던지는 시행의 사건 중 하나
ex2) 앞이 나오는 경우: {앞}은 동전을 던지는 시행의 사건 중 하나
④ 근원사건(atom)
- 표본공간의 단 하나의 성분으로 만들어지는 부분집합
ex1) 주사위를 던지는 시행의 근원사건: {1}, {2}, {3}, {4}, {5}, {6}
ex2) 동전을 던지는 시행의 근원사건: {앞}, {뒤}
2. 확률의 뜻
① 어떤 일이 발생할 것으로 기대되는 정도를 나타내는 수치
P(E), probability of E = m/n = 사건 E에 포함된 성분 개수/표본공간 U= \(\{e_{1}, e_{2}, ..., e_{n}\}\)에 포함된 성분개수
* 단, 표본공간 U에서 각 근원사건 \(\{e_{1}\}\), \(\{e_{2}\}\), ..., \(\{e_{n}\}\) 중 각 사건이 일어날 가능성은 모두 동등하다.
② 어떤 시행에 A, B라는 두 사건이 있다고 할 때
- A, B의 곱사건(product event) → A와 B가 동시에 발생하는 사건, \(A\cap B\)
- A, B의 합사건(sum event) → A 또는 B가 발생하는 사건, \(A\cup B\)
③ 합사건의 확률
$$ P(A\cup B)=P(A)+P(B)-P(A\cap B) $$
④ 확률의 덧셈정리(addition theorem)
- 사건 A, B가 서로 배반사건(exclusive event) 일 때 다음이 성립
$$ P(A\cup B)=P(A)+P(B) $$
⑤ 여사건의 확률(complementary event)
- 사건 A가 있을 때 A가 일어나지 않는 사건
$$ P(\bar{A})=1 - P(A) $$
3. 독립시행의 확률
- 예를 들어 나는 동전을 던지고 친구는 주사위를 던진다고 하자. 이 때 내가 동전을 던지는 시행과 친구가 주사위를 던지는 시행의 결과를 서로 영향을 미치지 않는다.
- 이렇게 몇개의 시행이 있고 어떤 시행의 결과도 다른 시행의 결과에 영향을 미치지 않을때(관계가 없을 때) 각 시행을 독립시행(independent trial)이라고 부른다. (* 반대는 종속시행(dependent trial))
① 독립인 두 시행 \(T_{1}\), \(T_{2}\)에 대해 시행 \(T_{1}\)에서는 사건 A가 발생하고 시행 \(T_{2}\)에서는 사건 B가 발생하는 사건을 C라고 할 때 사건 C가 발생할 확률은
$$ P(C) = P(A) \cdot P(B) $$
② 독립시행 3개 \(T_{1}\), \(T_{2}\), \(T_{3}\),가 있을 때 \(T_{1}\),에서는 사건 A가 일어나고 \(T_{2}\)에서는 사건 B가 일어나고 \(T_{3}\)에서는 사건 C가 일어난다라는 사건을 사건 D라고 하면
$$ P(D) = P(A) \cdot P(B) \cdot P(C) $$
4. 배반사건 독립사건 차이


5. 조건부 확률
사건 A가 발생했을 때 사건 B가 발생할 확률은 \(P_{A}(B)\)로 표기하고 일반적으로 이를 사건 A가 일어났을 때 사건 B가 일어날 조건부 확률(conditional probability)이라 부른다.
$$ P_{A}(B)=P(A \mid B)=\frac{P(A\cap B)}{P(A)} $$
① 확률의 곱셈정리(multiplication rule)
두 사건 A, B가 함께 일어날 확률은 다음과 같다.
$$ P(A\cap B) = P(A) \cdot P_{A}(B) $$
만약 사건 A와 B가 서로 독립이면
$$ P(A\cap B) = P(A) \cdot P(B) $$
② 베이즈 정리(원인의 확률)
$$ P_{B}(A)=\frac{P(A\cap B)}{P(A\cap B) + P(\bar{A}\cap B)} $$
→ A가 '원인'이고 B가 '결과'라고 하면
= B가 일어났을 때 A가 일어날 확률, \(P_{B}(A)\)
= 어떤 결과 (B)가 일어났을 때 어떤 원인(A)이 일어날 확률
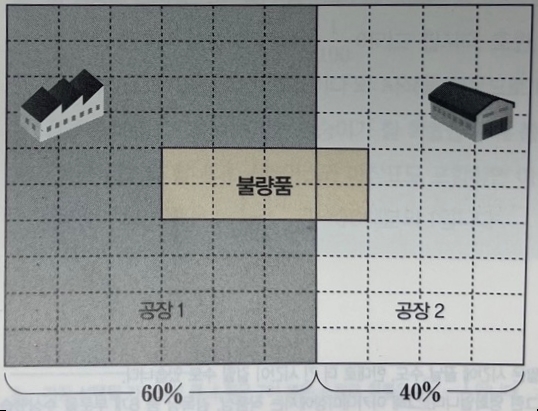
예) 공장1에서 만들어진 제품을 뽑을 때(A) 제품이 불량일 확률(B) = \(P_{A}(B)\)
뽑은 제품이 불량품이었을 때(B) 그 제품이 공장 1에서 만들어진 제품일(A) 확률 = \(P_{B}(A)\)
References:
[1] 다시 확률 통계 (확률), 나가노 히로유키, 길벗
[2] https://www.youtube.com/watch?v=7eGaNMamdQs
[3] https://www.youtube.com/watch?v=qZyb_40-Q5U&t=565s
'인공지능 수학 > 확률 및 통계' 카테고리의 다른 글
| 확률통계(2) - 기술통계 (0) | 2022.08.15 |
|---|

