| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- cnn
- Bert
- Ai
- ML
- Tokenization
- AI Fairness
- MLOps
- gpt2
- 인공지능 신뢰성
- word2vec
- 자연어
- 딥러닝
- GPT
- 지피티
- fairness
- GPT-3
- 설명가능성
- 챗GPT
- 머신러닝
- 챗지피티
- nlp
- 트랜스포머
- Transformer
- ChatGPT
- DevOps
- 신뢰성
- 케라스
- XAI
- trustworthiness
- 인공지능
- Today
- Total
research notes
규제 (Regularization) 본문
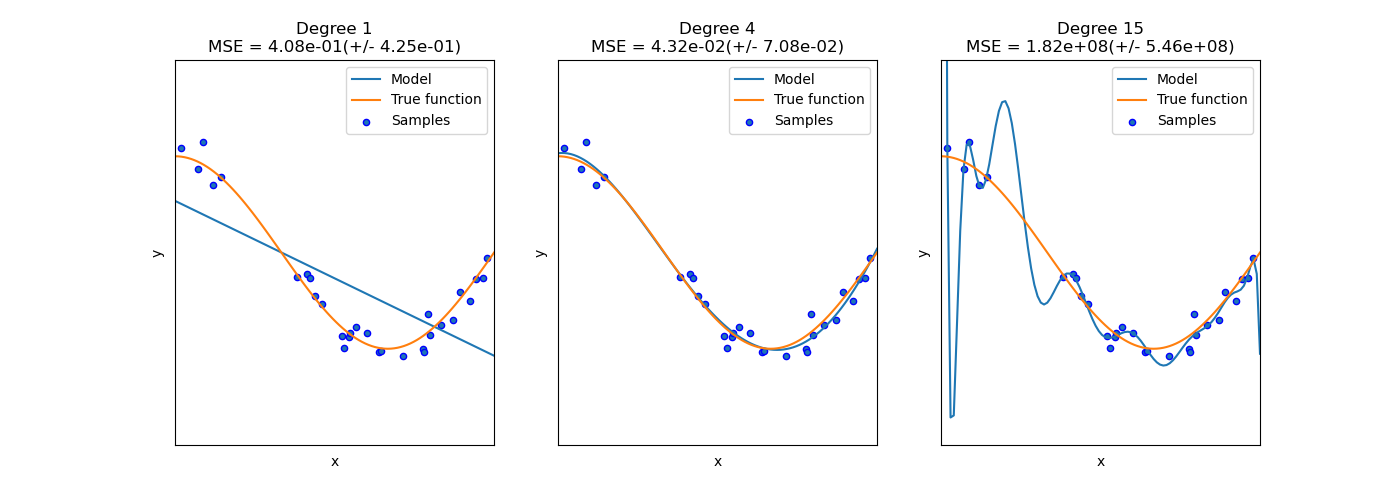
위 예는 과소적합과(Underfitting) 과적합의(Overfitting) 문제를 보여줌과 동시에 비선형(non-linear) 함수를 근사화하기 위해 어떻게 다항 선형 회귀를 사용할 수 있는지 방법을 보여준다. 플롯은 근사화하려는 코사인 함수의 일부, 실제 함수의 샘플 및 다른 근사하려는 모델을 표시하고 있다. 먼저 선형함수(차수가 1인 다항식)가 훈련 샘플에 적합하지 않음을 알 수 있는데 이것을 과소적합이라고 한다. 차수가 4인 다항식은 실제 함수에 거의 완벽하게 근사하지만, 더 높은 차수의 모델은 훈련 데이터에 과적합된다. 즉, 훈련 데이터의 노이즈를 학습한다. 교차검증을(cross-validation) 이용하여 과적합/과소적합을 정량적으로 평가할 수 있다. 검증세트에서 평균 제곱 오차(MSE)를 계산하고 그 값이 높을수록 훈련 데이터에 대한 모델의 일반화 될 가능성이 낮아진다 [2].
선형회귀 모델은 지나치게 모든 데이터에 적합한 회귀식을 만들기 위해서 다항식이 복잡해지고 회귀 계수가 매우 크게 설정되어 과대적합이 될 수 있다. 따라서, 평가 데이터 세트에 대해서 형편없는 예측 성능을 보일 수 있다. 그러므로 회귀 모델은 적절히 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어할 수 있어야 한다.(→ 규제의 필요성)
규제(Regularization) 방법에 따라 별도의 유형으로 나뉘며, 규제는 일반적인 선형회귀의 과적합 문제를 해결하기 위해서 회귀 계수에 패널티 값을 적용하는 것을 말한다.
- 회귀 모델은 적절히 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어할 수 있어야 한다.
- 최적 모델을 위한 Cost 함수 구성요소 = 학습데이터 잔차 오류 최소화 + 회귀계수 크기제어
- 이를 반영해 비용함수는 학습 데이터의 잔차 오류 값을 최소로 하는 RSS 최소화 방법과 과적합을 방지하기 위해 회귀계수 값이 커지지 않도록 하는 방법이(규제) 서로 균형을 이루어야 한다.
- 비용함수 목표 = Min(RSS (W) + alpha * ||W||)
- 비용함수에 alpha 값으로 패널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 규제(Regularization)라고 한다.
- alpha가 0(또는 매우 작은 값)이라면 비용함수 식은 기존과 동일한 Min(RSS(W) + 0) 이 될 것이다.
- alpha가 무한대(또는 매우 큰 값)라면 비용함수 식은 RSS(W)에 비해 alpha * ||W|| 값이 너무 커지게 되므로 W값을 0(또는 매우 작게)으로 만들어야 Cost가 최소화 되는 비용함수 목표를 달성할 수 있다.
- 일반 선형 회귀: 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화 할 수 있도록 회귀 계수를 최적화하며, 규제(Regularization)를 적용하지 않은 모델
- 라쏘(Lasso): 라쏘 회귀는 선형회귀에 L1 규제를 적용한 방식이다. L2 규제가 회귀 계수 값의 크기를 줄이는 데 반해, L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것이다. 이러한 특성 때문에 L1 규제는 피처 선택 기능으로도 불린다.

- 릿지(Ridge): 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델이다. 릿지 회귀는 L2 규제를 적용하는데, L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해서 회귀 계수값을 더 작게 만드는 규제 모델이다.

- 엘라스틱넷(ElasticNet): L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터 세트에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정한다.
References:
[1] 파이썬 머신러닝 완벽가이드, 권철민, 위키북스
[2] https://scikit-learn.org/stable/auto_examples/model_selection/plot_underfitting_overfitting.html
'머신러닝 > ML basic' 카테고리의 다른 글
| K-평균 알고리즘(K-Means Clustering) (0) | 2022.02.11 |
|---|---|
| Validation data set는 모델 학습에 사용이 되는가? (0) | 2022.02.05 |
| 성능평가지표 (Evaluation Metric) (0) | 2022.01.30 |
| 사이킷런 정리 (0) | 2022.01.28 |
| Numpy/Pandas 정리 (0) | 2022.01.28 |




