| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- cnn
- MLOps
- 자연어
- 인공지능
- 설명가능성
- 케라스
- Transformer
- trustworthiness
- ChatGPT
- 챗GPT
- 머신러닝
- Tokenization
- word2vec
- ML
- 신뢰성
- Ai
- Bert
- GPT-3
- XAI
- gpt2
- 딥러닝
- 챗지피티
- fairness
- 트랜스포머
- GPT
- nlp
- DevOps
- 지피티
- AI Fairness
- 인공지능 신뢰성
- Today
- Total
research notes
오차역전파(Backpropagation)-1 본문
1. 수치 미분(numerical differentiation)
미분은 극한으로 짧은시간(순간)에서의 변화량을 뜻한다. 예) 물체의 시간에 따른 위치 변화율(위치의 미분) ⇒ 속도
매우 미세한 차이를(ex. h=0.0001) 이용하여 함수의 변화량을 구하는 방법을 수치 미분이라고 한다.
수치 미분의 결과에는 오차가 포함되어 있을 뿐만아니라 수백만 개 이상의 매개변수를 사용하는 신경망과 같이 변수가 여러 개인 함수를 미분 할 경우 변수 각각을 미분해야 하기 때문에 계산량이 많다는 문제점이 있다(현실적이지 않다). ⇒ 역전파의 등장

2. 연쇄법칙(Chain rule)
역전파를 이해하는 열쇠는 연쇄법칙이다.
y=F(x)는 a=A(x), b=B(a), y=C(b)라는 세 함수로 구성된 합성 함수이며 이 때의 계산 그래프는 다음과 같다.

이 때 x에 대한 y의 미분은 다음과 같다.

위 식에서 알 수 있듯이 x에 대한 y의 미분은 구성 함수 각각의 미분값을 모두 곱한 것과 같다. 즉, 합성 함수의 미분은 각 함수의 국소적인 미분들로 분해할 수 있다. ⇒ 연쇄법칙
3. 역전파 원리

머신러닝은 주로 대량의 매개변수를 입력 받아서 마지막에 손실 함수(loss function)를 거쳐 출력을 내는 형태로 진행된다. 손실 함수의 출력은 (많은 경우) 단일한 스칼라 값이며(y) 오차역전파시 손실 함수의 각 매개변수에 대한 미분을 계산해야 한다. 이런 경우 미분값을 출력에서 입력 방향으로 전파하면 한 번의 전파만으로 모든 매개변수에 대한 미분을 계산 할 수 있다. 또한, 아래 그림은 곱셈의 순전파와(위) 역전파(아래)에 대해 나타낸다.
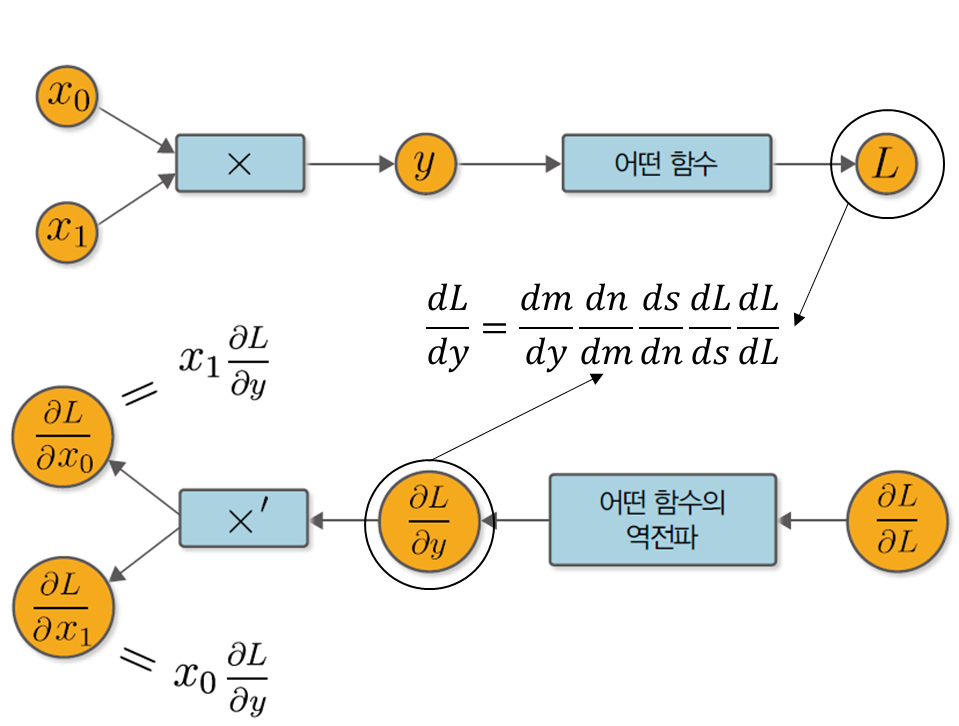
4. 행렬 곱의 역전파
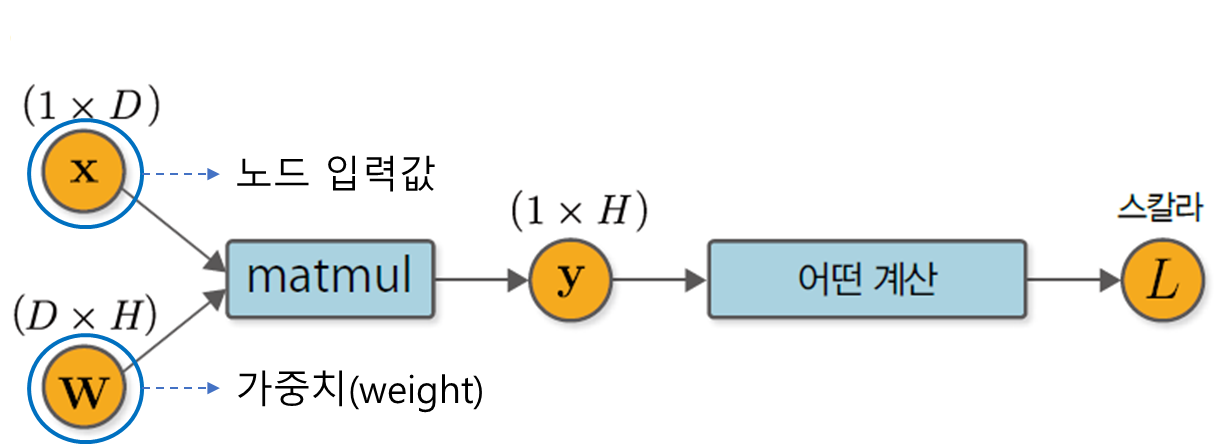
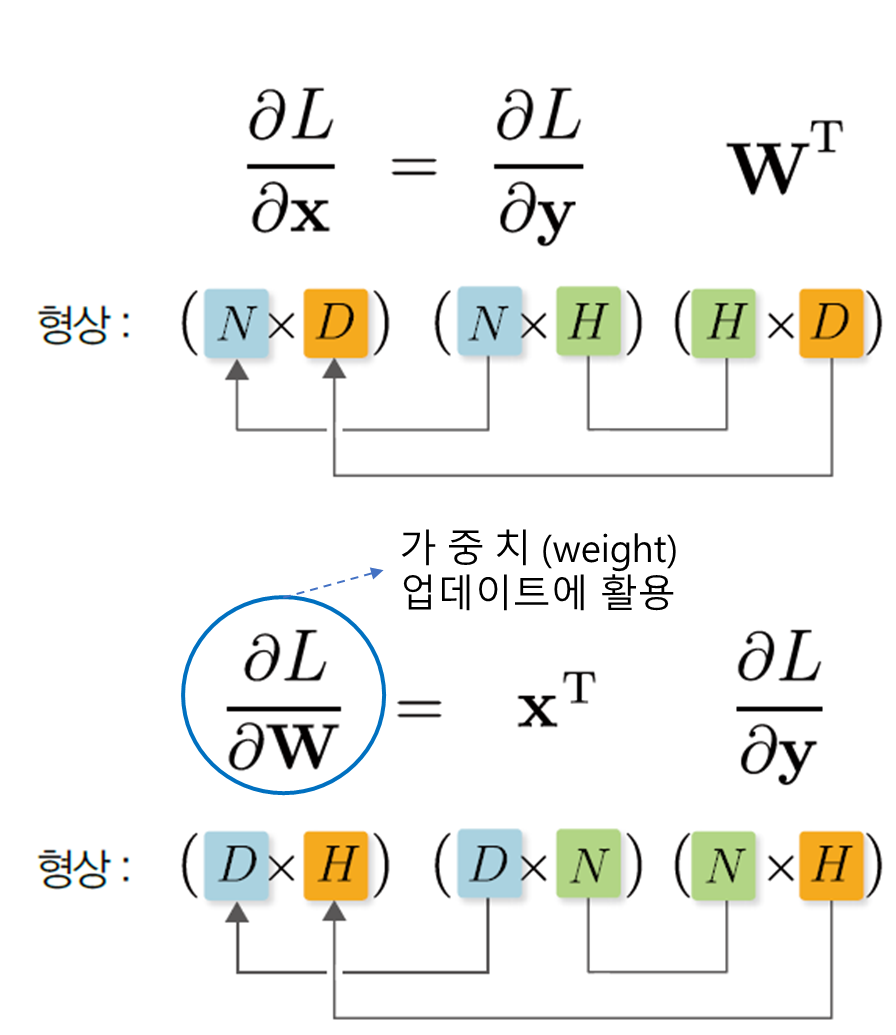
위 구조에서
위 식의
위 식에서
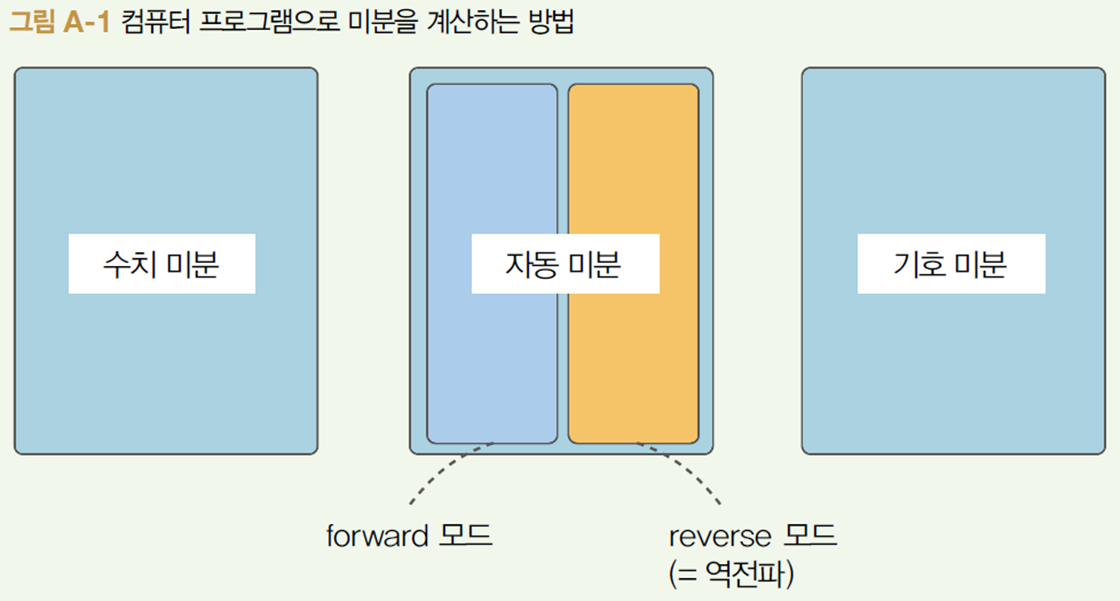
5. 자동 미분
컴퓨터 프로그램에서 미분을 계산하는 방법은 크게 세 가지로 나눌 수 있다.
① 수치 미분(numerical differentiation)
- 수치 미분은 변수에 미세한 차이를 주어 일반적인 계산(순전파)을 2회 실시하고 두 출력의 차이로부터 근사적으로 미분을 계산
- 수치 미분은 구현하기 쉽지만 출력에 오차가 포함되기 쉽고 다량의 변수를 사용하는 함수를 다룰 때는 계산 비용이 높다는 단점이 있다.
② 기호 미분(symbolic differentiation)
- 기호 미분은 고등학교 수학에서 배운 것처럼 미분 공식을 이용하여 계산하는 방법이며 입력도 '수식'이고 출력도 '수식(도함수)'이다.
- 딥러닝에서 취급하는 계산은 수많은 변수에 대한 수식이 아닌 미분'값'을 효율적으로 구하는 것이므로 다른 효율적인 방법이 필요
③ 자동 미분(automatic differentiation)
- 자동 미분은 연쇄 법칙을 사용하여 미분하는 방법이며 역전파 방식도 자동 미분에 속한다.
References:
[1] 밑바닥부터 시작하는 딥러닝 3, 한빛미디어
'인공지능 수학 > 미분적분' 카테고리의 다른 글
| 오차역전파(Backpropagation)-2 (0) | 2022.06.12 |
|---|---|
| 적분(integral) 정리 (0) | 2022.06.01 |
| 테일러 급수(Taylor Series) (0) | 2022.05.22 |



